Search
CBC Encryption
Wed Mar 25, 2015 6:41 pm by ORLP2
For those who don't know me, I am ORLP (lowercase or upper-case will do, I honestly aren't fussed). I am a Computer Science and cryptography enthusiast. I am looking to broaden my horizon within the "computer security" scene, even if that means joining a newly-crafted forum to get my name across and meet other people who have similar interests as me.
I would like to start by saying I'm …
I would like to start by saying I'm …
Comments: 0
Operating System Poll
Tue Mar 17, 2015 7:34 pm by Orianthi
So what operating systems do y'all use?
I use: Windows(7), Linux(Debian, Ubuntu, Mint, Arch Linux, Bieban, Fedora), OS X(Yosemite, Maveriks)
I use: Windows(7), Linux(Debian, Ubuntu, Mint, Arch Linux, Bieban, Fedora), OS X(Yosemite, Maveriks)
Comments: 0
Who is online?
In total there are 5 users online :: 0 Registered, 0 Hidden and 5 Guests None
Most users ever online was 14 on Mon Jun 01, 2020 9:21 pm
CBC Encryption
Page 1 of 1
 CBC Encryption
CBC Encryption
For those who don't know me, I am ORLP (lowercase or upper-case will do, I honestly aren't fussed). I am a Computer Science and cryptography enthusiast. I am looking to broaden my horizon within the "computer security" scene, even if that means joining a newly-crafted forum to get my name across and meet other people who have similar interests as me.
I would like to start by saying I'm not looking to "impress" any of you, that's not why I'm here. I'm here because I generally enjoy the field I'm in and want to share my knowledge with those who want to learn new things. :-)
I recently read an article regarding laravel cookie forgery, decryption, and remote code execution. In this article, the author was able to use CBC-R(Oracle padding attack) to encode an arbitrary serialized object, without knowing the key. The concept of exploiting unserialize functions is somewhat straightforward for me, however, the CBC-R aspect of this was not so straight forward as he didn't explain in enough detail.. So I thought that I would publish something for others to come across and read in an attempt to allow those who want to expand their knowledge to comprehend what is written.
*** If you have any questions, feel free to ask me, I don't bite**
Let's do it in several steps so that I don't confuse anybody. First, I'll start with CBC encryption and IV so I'm splitting it into different sections.
Now, for those who don't know, CBC encryption is a block cipher mode of operation, which is best explained with a drawing that I shamelessly plunder from the Wikipedia page, and reproduce here for ease of reading:
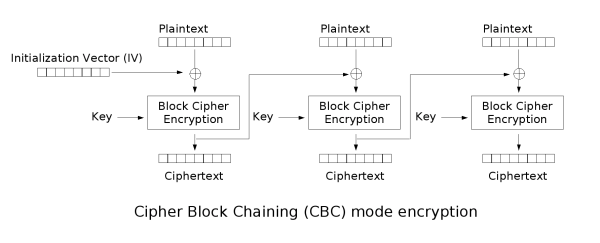
With CBC encryption, the block cipher is used to encrypt each block of data; however, to avoid leaking information about identical plaintext blocks (see the famous penguin picture as an illustration of why this is a problem in practice), CBC includes some "randomization" of data, by XORing each plaintext block, before encryption, with the previous encrypted block. Since the first block has no "previous encrypted block", a synthetic one must be provided; that is the IV. Decryption works in the obvious way, which is made explicit in this drawing:

Since the IV must be known to the decryption engine, it must be provided with the ciphertext. It must not be a fixed value because security of CBC relies on the IV being uniformly random, with a new one for each message.
In this case, the block cipher is Rijndael. Rijndael is the basis for AES. Specifically, when NIST called for candidate functions for their new standard (to be a successor to DES and 3DES), they wanted a block cipher working with blocks of 128 bits, and accepting keys of 128, 192 or 256 bits. The Rijndael submitters proposed more: the algorithm accepted the three key sizes, but also had variants for blocks of 128, 192 and 256 bits. Rijndael was chosen as AES (among a total of 15 candidates), with the NIST requirements, i.e. blocks of 128 bits only. AES is then a strict subset of the Rijndael family of algorithms.
The Laravel designers decided to use Rijndael as the block cipher, with the largest block that Rijndael can support, i.e. 32 bytes (256 bits). Why they insisted on such large blocks is unclear to me, but that was probably on the assumption that "larger is better", which is scientifically unsubstantiated. For security, we need "large enough" blocks: the security of most modes begins to break down when we encrypt more than 2n/2 blocks of n bits (with a given key). With n = 128, this leaves room for about 300 millions of terabytes, which ought to be sufficient; larger blocks are unnecessary. In fact, one may even claim that Rijndael with 32-byte blocks is less secure than AES in the following sense: all the analysis performed by cryptographers over the last 15 years concentrated on the variation with 128-bit blocks (the AES proper), and the other sizes have been mostly neglected.
**Note: since Laravel fixed their code, all I say here is about a past version of Laravel, from last year.**
By now you should all know that CBC can encrypt only some input message whose size is a multiple of the block size. To encrypt a sequence of bytes of arbitrary length, there must be some sort of padding: extra bytes added to reach a size that can be processed by the CBC encryption engine. However, such padding must be unambiguous enough so that the receiver knows where data stops and where padding begins. Sometimes it is sufficient to add some bytes to inconsequential value, if the inner message is self-terminated; however, in general, encryption engines aim at encrypting arbitrary sequences of bytes, whose end cannot necessarily be determined internally. The most common convention, which is used here, is called PKCS#7 padding:
1. At least 1, and at most b bytes are added, where b is the block size (in bytes).
2. When x bytes are added, all the bytes have value x.
The receiver, after decrypting, reads the last message byte, which contains x and thus unambiguously documents the actual padding length, allowing its removal. Some decryption engines (not all) will also check that all padding bytes have the same value x; others will just use the value of the last byte and ignore the rest.
There are variants. For instance, some protocols define that the value of the added bytes shall be x-1 if x bytes are added. Also, some protocols (e.g. SSL 3.0, as opposed to TLS 1.0 and later versions) explicitly state that only the last byte contains x, and the other bytes may have arbitrary contents.
Crucially, padding removal may fail. The receiver expects the last byte to contain a value x which has a value between 1 and b; some receivers also expect all last x bytes to have value x. Here, the decryption engine applies the latter rule: it will complain if any of the last x bytes contains any value other than x. A padding oracle attack is an attack where the attacker can submit messages which are purportedly encrypted with a key K (that the attacker does not know), but really were crafted by the attacker; and the decryption engine leaks a single binary information: whether decryption yielded a correct padding or not. Typically, the receiver returns an error message, and not the same error message in two cases:
1. After CBC decryption, no well-formed padding was found.
2. After CBC decryption, well-formed padding was found, but after padding removal, the conveyed data turned out to be unreadable junk.
Now.. I'm moving on to messuage auth code. For those who don't know (again), message authentication code is a cryptographic algorithm which aims at ensuring data integrity.
It can be envisioned as a "checksum with a key". In general, when there are attackers, then there are active attackers, who can modify messages while in transit or try to send handcrafted malicious messages; hence, where encryption is required, a MAC is probably needed too.
There has been some considerable work on how encryption and a MAC shall be assembled together. Today, we recommend using a mode which combines both in a single unit (e.g. GCM), but the old-style method was to glue together an encryption system (typically a block cipher in CBC mode) and a stand-alone MAC (traditionally HMAC). This glue-ing can be done in about three ways, called MAC-then-encrypt, MAC-and-encrypt, and encrypt-then-MAC. The last one is the right one; done properly, it prevents large classes of attacks, including, indeed, padding oracle attacks. See this question on the crypto.SE site for more discussion on this.
Turns out that the Laravel people used encrypt-then-MAC but botched it. In encrypt-then-MAC, the data is first encrypted, then the MAC is applied on the encrypted message. This prevents oracle padding attacks and, more generally, all "crafted message" attacks, because the MAC will be checked before decryption, thus ruthlessly killing out all such malicious messages without even letting them reach the decryption stage, let alone the padding removal stage. However, such a MAC works only if it is applied to everything that is used to decrypt, and that should include the IV.
The Laravel people forgot to include the IV in the MAC input. Their MAC (which is HMAC) is computed over the encrypted blocks only. The consequence is that the attacker can modify the IV at will, and the MAC won't see it. But modifying the IV gives a lot control over the first block of plaintext. Indeed, the decryption engine, upon receiving IV and the ciphertext blocks C1, C2,..., will computed the plaintext as:
-> P1 = IV xor DK(C1)
-> P2 = C1 xor DK(C2)
-> P3 = C2 xor DK(C3)
-> ...
Since the MAC is computed over the Ci blocks, the attacker cannot modify them (this would invalidate the MAC), but he can choose the IV. If the person knows the original plaintext block P1, then that person can "alter" it to any other value by modifying the IV. In this case, this means that the first 32 bytes of the message can be chosen by the attacker. Since the Laravel cookie contents are, basically, the user ID, control over the first 32 bytes is more than enough to allow arbitrary user impersonation, which is already bad.
(Ironically, the use of overlarge 32-byte blocks actually gives more power to the attacker, so really using AES and its 16-byte blocks would have been better. However, the true weakness is the improper MAC application.)
a second, and arguably more serious, issue in laravel's code is that its MAC verification can essentially be disabled. This is explained in the article:
"Another problem with the MAC verification code is that the comparison is done with a non-strict operator: !=. This means that PHP will attempt type juggling prior to the actual equality check. The output of the hash_hmac() function is always a string, but if $payload['mac'] is an integer then the type coercion can make it relatively easy to forge a matching MAC. For example, if the true MAC starts with “0” or a non-numeric character then the integer zero will match, if it starts “1x” (where “x” is non-numeric) then the integer 1 will match, and so on.
var_dump('abcdefg' == 0); // true
var_dump('1abcdef' == 1); // true
var_dump('2abcdef' == 2); // true
Since the MAC is from the result of a call to json_decode() an attacker can provide an integer. This makes it quite likely that an attacker is able to provide a ‘valid’ MAC for an arbitrary ciphertext."
So now we can assume that the attacker can modify the IV and all ciphertext blocks at will, without incurring the wrath of the MAC.
We now come to the juicy part.
-> There is a server, using Laravel, which has an internal secret key K that the attacker does not know.
-> The server uses cookies, which are encrypted with K.
-> When the server decrypts a cookie, it does so as explained above, and it acts as a padding oracle. Specifically, since the server uses PHP's unserialize() magic, it will respond on some alleged (but altered) cookie with one of these two conceptual messages:
-> There was no syntactically valid padding.
-> I found a proper padding, but then the decryption result was some junk of length xxx bytes.
The attacker can thus not only learn whether his message resulted in a proper padding, but also what was the exact padding length in that case.
-> If the server succeeds at decrypting a cookie, and found a valid padding, then the contents can actually trigger arbitrary code execution on the server. This is more unserialize() magic.
The attacker's goal is thus now to handcraft an encrypted cookie value which, when decrypted, contains a properly padded payload which runs nefarious code on the server. All of CBC-R is about exploiting the padding oracle into computing such encryption. Pay attention: this is the tricky part.
For one block:
Suppose that the attacker is given two block values T and V. These are two b-byte sequences. The attacker wants to compute a third block value U such that:
T = U xor DK(V)
Why would the attacker want to do that? This is actually forging of an encrypted message with chosen contents. The equation above is the decryption core: if the attacker finds T, then the message consisting of IV U and encrypted block V decrypts to T. In that sense, the attacker tries to work out an encrypted version of message T.
Let's see how it works. The attacker will first send a one-block cookie to the server with some random IV and one encrypted block V; but he will force the last IV byte to have value 0x00. With high probability, the server will answer with the "bad padding" error. The attacker then tries again with the same IV, except for the last IV byte that he forces to 0x01. If that fails again, then he tries with 0x02, and so on.
Suppose that the last byte of DK(V) is 0x42. When the attacker tries a forged cookie such that the last byte of the IV is 0x43, the decryption engine will obtain a plaintext block ending with 0x42 xor 0x43, i.e. the value 0x01. Now that is a syntactically valid PKCS#7 padding. The error message from the server changes: it no longer is "bad padding" but "junk decrypted contents". The attacker sees that, and concludes that decryption found a valid padding, and thus infers that the last byte of DK(V) is 0x42.
Since we have 32-byte blocks, we number bytes from 0 to 31 within a block. The attacker has just learned that the byte 31 of DK(V) has value 0x42 (in that example). He now wishes to obtain byte 30. For that, he will send one-block cookies, still with encrypted block V; he will force byte 31 of the IV to 0x40, and set byte 30 of the IV to 0x00. Setting byte 31 of the IV to 0x40 means that, upon decryption, that 0x40 will be XORed with byte 31 of DK(V), that is known to have value 0x42. The result of that XOR will then be 0x02. The attacker then sends such one-byte cookies, setting IV byte 30 to 0x00, 0x01, 0x02... until the error message from the server switches again from "bad padding" to "junk decrypted contents". When will this happen ?
Suppose that byte 30 of DK(V) has value 0xC7. When the attacker tries one of his forged cookies such that the IV ends with 0xC5 0x40, the decryption engine will XOR that with DK(V), a value that ends with 0xC7 0x42. The XOR result will then end with 0x02 0x02, which again is a valid PKCS#7 padding (of length 2 bytes), resulting in the visible error message change. Now the attacker has obtained byte 30 of of DK(V).
Iterate. The attacker knows bytes 30 and 31 of DK(V), and tries IV values whose last two bytes are 0xC4 0x41, because these yield 0x03 0x03 upon decryption-and-XOR. The attacker cycles through the possible values for byte 29, until the 3-byte PKCS#7 padding (0x03 0x03 0x03) is reached. And so on...
That way, the attacker ends up with complete knowledge of DK(V). This requires an average of 128 requests per byte (there are 256 possible values for a byte, and the attacker will reach the right one after trying half of them on average), so 128*32 = 4096 requests for the complete block. This can take a few seconds or minutes, depending on the network speed, the processing power of the server, and the will of the attacker to remain as stealthy as possible.
When the attacker knows the complete DK(V), he just has to compute:
U = T xor DK(V)
-> which yields the sought after value for U.
For several blocks:
With the one-block attack described above, the attacker can now obtain an encrypted version of an arbitrary multi-block message.
Let's suppose that the attacker has a multi-block message P1, P2,... Pr. There are r blocks. That message is the payload with the PHP thingies which result into remote code execution, with proper padding already applied. The attacker wants to find C0, C1,... Cr such that a cookie consisting of:
-> the IV of value C0
-> the encrypted blocks C1 to Cr
will be decrypted by the server into P1, P2,... Pr.
The attacker proceeds right to left:
-> The attacker chooses a random value for Cr.
-> Given Cr and Pr, the attacker wants to find Cr-1 such that:
-> Pr = Cr-1 xor DK(Cr)
---> This is exactly the context of the one-block attack from the previous section, with T = Pr and V = Cr. Thus, the attacker runs the one-block attack and obtains Cr-1.
-> Given Cr-1 and Pr-1, the attacker wants to find Cr-2 such that:
-> Pr-1 = Cr-2 xor DK(Cr-1)
Again, this maps to the one-block attack, with T = Pr-1 and V = Cr-1. The one-block attack yields Cr-2.
-> The attacker iterates. He gets Cr-3, Cr-4, and so on, down to C0.
-> The attacker has his complete message, and sends it to the server, and hijacks it. Endgame.
The core issue in the (old) lavarel code is an improperly applied MAC. A MAC which:
-> is applied in the encrypt-then-MAC way;
-> without forgetting to also send the IV in the MAC input;
-> and is verified without possibility of cancelling it with some PHP type-juggling;
will effectively prevent any kind of padding oracle attack.
Lacking a good MAC, someone might try to make sure that the decryption engine does not leak information about the padding. This is hard: if no padding is found, then the engine has to conjure some synthetic data so as to continue processing; but subsequent steps must not yield recognizable error messages when that "synthetic data" fails to decode. Moreover, demonstrations have been made (in lab conditions) of timing attacks in which the oracle consisted in the minute difference in processing time between the processing of a "good padding" vs a "bad padding". When the attacker is on the same LAN as the server, timing differences down to the microsecond can be measured.
The CBC-R reconstruction method works for any kind of CBC padding oracles, although there are variations depending on the exact species of padding (in particular whether the decryption engine checks that all x last bytes have the same value or not). This can be applied wherever CBC-based decryption occurs without protection of a MAC. In the case of the Laravel framework, this was for cookies, and the lack of MAC was due to both improper computations, and the creative featurism of PHP. The same kind of padding oracle attacks has been applied in other contexts; the original description, back in 2002 (by Serge Vaudenay), was on SSL records. Rizzo and Duong popularized it in 2010 by showing how it applied well on ASP.NET.
This incidentally illustrates that a Javascript demo with a Youtube video can be a powerful path to fame even when the original research was done by somebody else 8 years ago. I guess this means that we need both really smart researchers like Serge, and determinate implementers who go to the trouble of understanding the research, and then applying it to practical cases, working out the zillions of practical implementation details. Theory and experimentation are two sides of Science and both are required to make things change.
Thank you for those who decided to read my long thread, I appreciate you sitting through it all, and hopefully you've learned something new :')
I would like to start by saying I'm not looking to "impress" any of you, that's not why I'm here. I'm here because I generally enjoy the field I'm in and want to share my knowledge with those who want to learn new things. :-)
I recently read an article regarding laravel cookie forgery, decryption, and remote code execution. In this article, the author was able to use CBC-R(Oracle padding attack) to encode an arbitrary serialized object, without knowing the key. The concept of exploiting unserialize functions is somewhat straightforward for me, however, the CBC-R aspect of this was not so straight forward as he didn't explain in enough detail.. So I thought that I would publish something for others to come across and read in an attempt to allow those who want to expand their knowledge to comprehend what is written.
*** If you have any questions, feel free to ask me, I don't bite**
Let's do it in several steps so that I don't confuse anybody. First, I'll start with CBC encryption and IV so I'm splitting it into different sections.
Now, for those who don't know, CBC encryption is a block cipher mode of operation, which is best explained with a drawing that I shamelessly plunder from the Wikipedia page, and reproduce here for ease of reading:

With CBC encryption, the block cipher is used to encrypt each block of data; however, to avoid leaking information about identical plaintext blocks (see the famous penguin picture as an illustration of why this is a problem in practice), CBC includes some "randomization" of data, by XORing each plaintext block, before encryption, with the previous encrypted block. Since the first block has no "previous encrypted block", a synthetic one must be provided; that is the IV. Decryption works in the obvious way, which is made explicit in this drawing:

Since the IV must be known to the decryption engine, it must be provided with the ciphertext. It must not be a fixed value because security of CBC relies on the IV being uniformly random, with a new one for each message.
In this case, the block cipher is Rijndael. Rijndael is the basis for AES. Specifically, when NIST called for candidate functions for their new standard (to be a successor to DES and 3DES), they wanted a block cipher working with blocks of 128 bits, and accepting keys of 128, 192 or 256 bits. The Rijndael submitters proposed more: the algorithm accepted the three key sizes, but also had variants for blocks of 128, 192 and 256 bits. Rijndael was chosen as AES (among a total of 15 candidates), with the NIST requirements, i.e. blocks of 128 bits only. AES is then a strict subset of the Rijndael family of algorithms.
The Laravel designers decided to use Rijndael as the block cipher, with the largest block that Rijndael can support, i.e. 32 bytes (256 bits). Why they insisted on such large blocks is unclear to me, but that was probably on the assumption that "larger is better", which is scientifically unsubstantiated. For security, we need "large enough" blocks: the security of most modes begins to break down when we encrypt more than 2n/2 blocks of n bits (with a given key). With n = 128, this leaves room for about 300 millions of terabytes, which ought to be sufficient; larger blocks are unnecessary. In fact, one may even claim that Rijndael with 32-byte blocks is less secure than AES in the following sense: all the analysis performed by cryptographers over the last 15 years concentrated on the variation with 128-bit blocks (the AES proper), and the other sizes have been mostly neglected.
**Note: since Laravel fixed their code, all I say here is about a past version of Laravel, from last year.**
By now you should all know that CBC can encrypt only some input message whose size is a multiple of the block size. To encrypt a sequence of bytes of arbitrary length, there must be some sort of padding: extra bytes added to reach a size that can be processed by the CBC encryption engine. However, such padding must be unambiguous enough so that the receiver knows where data stops and where padding begins. Sometimes it is sufficient to add some bytes to inconsequential value, if the inner message is self-terminated; however, in general, encryption engines aim at encrypting arbitrary sequences of bytes, whose end cannot necessarily be determined internally. The most common convention, which is used here, is called PKCS#7 padding:
1. At least 1, and at most b bytes are added, where b is the block size (in bytes).
2. When x bytes are added, all the bytes have value x.
The receiver, after decrypting, reads the last message byte, which contains x and thus unambiguously documents the actual padding length, allowing its removal. Some decryption engines (not all) will also check that all padding bytes have the same value x; others will just use the value of the last byte and ignore the rest.
There are variants. For instance, some protocols define that the value of the added bytes shall be x-1 if x bytes are added. Also, some protocols (e.g. SSL 3.0, as opposed to TLS 1.0 and later versions) explicitly state that only the last byte contains x, and the other bytes may have arbitrary contents.
Crucially, padding removal may fail. The receiver expects the last byte to contain a value x which has a value between 1 and b; some receivers also expect all last x bytes to have value x. Here, the decryption engine applies the latter rule: it will complain if any of the last x bytes contains any value other than x. A padding oracle attack is an attack where the attacker can submit messages which are purportedly encrypted with a key K (that the attacker does not know), but really were crafted by the attacker; and the decryption engine leaks a single binary information: whether decryption yielded a correct padding or not. Typically, the receiver returns an error message, and not the same error message in two cases:
1. After CBC decryption, no well-formed padding was found.
2. After CBC decryption, well-formed padding was found, but after padding removal, the conveyed data turned out to be unreadable junk.
Now.. I'm moving on to messuage auth code. For those who don't know (again), message authentication code is a cryptographic algorithm which aims at ensuring data integrity.
It can be envisioned as a "checksum with a key". In general, when there are attackers, then there are active attackers, who can modify messages while in transit or try to send handcrafted malicious messages; hence, where encryption is required, a MAC is probably needed too.
There has been some considerable work on how encryption and a MAC shall be assembled together. Today, we recommend using a mode which combines both in a single unit (e.g. GCM), but the old-style method was to glue together an encryption system (typically a block cipher in CBC mode) and a stand-alone MAC (traditionally HMAC). This glue-ing can be done in about three ways, called MAC-then-encrypt, MAC-and-encrypt, and encrypt-then-MAC. The last one is the right one; done properly, it prevents large classes of attacks, including, indeed, padding oracle attacks. See this question on the crypto.SE site for more discussion on this.
Turns out that the Laravel people used encrypt-then-MAC but botched it. In encrypt-then-MAC, the data is first encrypted, then the MAC is applied on the encrypted message. This prevents oracle padding attacks and, more generally, all "crafted message" attacks, because the MAC will be checked before decryption, thus ruthlessly killing out all such malicious messages without even letting them reach the decryption stage, let alone the padding removal stage. However, such a MAC works only if it is applied to everything that is used to decrypt, and that should include the IV.
The Laravel people forgot to include the IV in the MAC input. Their MAC (which is HMAC) is computed over the encrypted blocks only. The consequence is that the attacker can modify the IV at will, and the MAC won't see it. But modifying the IV gives a lot control over the first block of plaintext. Indeed, the decryption engine, upon receiving IV and the ciphertext blocks C1, C2,..., will computed the plaintext as:
-> P1 = IV xor DK(C1)
-> P2 = C1 xor DK(C2)
-> P3 = C2 xor DK(C3)
-> ...
Since the MAC is computed over the Ci blocks, the attacker cannot modify them (this would invalidate the MAC), but he can choose the IV. If the person knows the original plaintext block P1, then that person can "alter" it to any other value by modifying the IV. In this case, this means that the first 32 bytes of the message can be chosen by the attacker. Since the Laravel cookie contents are, basically, the user ID, control over the first 32 bytes is more than enough to allow arbitrary user impersonation, which is already bad.
(Ironically, the use of overlarge 32-byte blocks actually gives more power to the attacker, so really using AES and its 16-byte blocks would have been better. However, the true weakness is the improper MAC application.)
a second, and arguably more serious, issue in laravel's code is that its MAC verification can essentially be disabled. This is explained in the article:
"Another problem with the MAC verification code is that the comparison is done with a non-strict operator: !=. This means that PHP will attempt type juggling prior to the actual equality check. The output of the hash_hmac() function is always a string, but if $payload['mac'] is an integer then the type coercion can make it relatively easy to forge a matching MAC. For example, if the true MAC starts with “0” or a non-numeric character then the integer zero will match, if it starts “1x” (where “x” is non-numeric) then the integer 1 will match, and so on.
var_dump('abcdefg' == 0); // true
var_dump('1abcdef' == 1); // true
var_dump('2abcdef' == 2); // true
Since the MAC is from the result of a call to json_decode() an attacker can provide an integer. This makes it quite likely that an attacker is able to provide a ‘valid’ MAC for an arbitrary ciphertext."
So now we can assume that the attacker can modify the IV and all ciphertext blocks at will, without incurring the wrath of the MAC.
We now come to the juicy part.
-> There is a server, using Laravel, which has an internal secret key K that the attacker does not know.
-> The server uses cookies, which are encrypted with K.
-> When the server decrypts a cookie, it does so as explained above, and it acts as a padding oracle. Specifically, since the server uses PHP's unserialize() magic, it will respond on some alleged (but altered) cookie with one of these two conceptual messages:
-> There was no syntactically valid padding.
-> I found a proper padding, but then the decryption result was some junk of length xxx bytes.
The attacker can thus not only learn whether his message resulted in a proper padding, but also what was the exact padding length in that case.
-> If the server succeeds at decrypting a cookie, and found a valid padding, then the contents can actually trigger arbitrary code execution on the server. This is more unserialize() magic.
The attacker's goal is thus now to handcraft an encrypted cookie value which, when decrypted, contains a properly padded payload which runs nefarious code on the server. All of CBC-R is about exploiting the padding oracle into computing such encryption. Pay attention: this is the tricky part.
For one block:
Suppose that the attacker is given two block values T and V. These are two b-byte sequences. The attacker wants to compute a third block value U such that:
T = U xor DK(V)
Why would the attacker want to do that? This is actually forging of an encrypted message with chosen contents. The equation above is the decryption core: if the attacker finds T, then the message consisting of IV U and encrypted block V decrypts to T. In that sense, the attacker tries to work out an encrypted version of message T.
Let's see how it works. The attacker will first send a one-block cookie to the server with some random IV and one encrypted block V; but he will force the last IV byte to have value 0x00. With high probability, the server will answer with the "bad padding" error. The attacker then tries again with the same IV, except for the last IV byte that he forces to 0x01. If that fails again, then he tries with 0x02, and so on.
Suppose that the last byte of DK(V) is 0x42. When the attacker tries a forged cookie such that the last byte of the IV is 0x43, the decryption engine will obtain a plaintext block ending with 0x42 xor 0x43, i.e. the value 0x01. Now that is a syntactically valid PKCS#7 padding. The error message from the server changes: it no longer is "bad padding" but "junk decrypted contents". The attacker sees that, and concludes that decryption found a valid padding, and thus infers that the last byte of DK(V) is 0x42.
Since we have 32-byte blocks, we number bytes from 0 to 31 within a block. The attacker has just learned that the byte 31 of DK(V) has value 0x42 (in that example). He now wishes to obtain byte 30. For that, he will send one-block cookies, still with encrypted block V; he will force byte 31 of the IV to 0x40, and set byte 30 of the IV to 0x00. Setting byte 31 of the IV to 0x40 means that, upon decryption, that 0x40 will be XORed with byte 31 of DK(V), that is known to have value 0x42. The result of that XOR will then be 0x02. The attacker then sends such one-byte cookies, setting IV byte 30 to 0x00, 0x01, 0x02... until the error message from the server switches again from "bad padding" to "junk decrypted contents". When will this happen ?
Suppose that byte 30 of DK(V) has value 0xC7. When the attacker tries one of his forged cookies such that the IV ends with 0xC5 0x40, the decryption engine will XOR that with DK(V), a value that ends with 0xC7 0x42. The XOR result will then end with 0x02 0x02, which again is a valid PKCS#7 padding (of length 2 bytes), resulting in the visible error message change. Now the attacker has obtained byte 30 of of DK(V).
Iterate. The attacker knows bytes 30 and 31 of DK(V), and tries IV values whose last two bytes are 0xC4 0x41, because these yield 0x03 0x03 upon decryption-and-XOR. The attacker cycles through the possible values for byte 29, until the 3-byte PKCS#7 padding (0x03 0x03 0x03) is reached. And so on...
That way, the attacker ends up with complete knowledge of DK(V). This requires an average of 128 requests per byte (there are 256 possible values for a byte, and the attacker will reach the right one after trying half of them on average), so 128*32 = 4096 requests for the complete block. This can take a few seconds or minutes, depending on the network speed, the processing power of the server, and the will of the attacker to remain as stealthy as possible.
When the attacker knows the complete DK(V), he just has to compute:
U = T xor DK(V)
-> which yields the sought after value for U.
For several blocks:
With the one-block attack described above, the attacker can now obtain an encrypted version of an arbitrary multi-block message.
Let's suppose that the attacker has a multi-block message P1, P2,... Pr. There are r blocks. That message is the payload with the PHP thingies which result into remote code execution, with proper padding already applied. The attacker wants to find C0, C1,... Cr such that a cookie consisting of:
-> the IV of value C0
-> the encrypted blocks C1 to Cr
will be decrypted by the server into P1, P2,... Pr.
The attacker proceeds right to left:
-> The attacker chooses a random value for Cr.
-> Given Cr and Pr, the attacker wants to find Cr-1 such that:
-> Pr = Cr-1 xor DK(Cr)
---> This is exactly the context of the one-block attack from the previous section, with T = Pr and V = Cr. Thus, the attacker runs the one-block attack and obtains Cr-1.
-> Given Cr-1 and Pr-1, the attacker wants to find Cr-2 such that:
-> Pr-1 = Cr-2 xor DK(Cr-1)
Again, this maps to the one-block attack, with T = Pr-1 and V = Cr-1. The one-block attack yields Cr-2.
-> The attacker iterates. He gets Cr-3, Cr-4, and so on, down to C0.
-> The attacker has his complete message, and sends it to the server, and hijacks it. Endgame.
The core issue in the (old) lavarel code is an improperly applied MAC. A MAC which:
-> is applied in the encrypt-then-MAC way;
-> without forgetting to also send the IV in the MAC input;
-> and is verified without possibility of cancelling it with some PHP type-juggling;
will effectively prevent any kind of padding oracle attack.
Lacking a good MAC, someone might try to make sure that the decryption engine does not leak information about the padding. This is hard: if no padding is found, then the engine has to conjure some synthetic data so as to continue processing; but subsequent steps must not yield recognizable error messages when that "synthetic data" fails to decode. Moreover, demonstrations have been made (in lab conditions) of timing attacks in which the oracle consisted in the minute difference in processing time between the processing of a "good padding" vs a "bad padding". When the attacker is on the same LAN as the server, timing differences down to the microsecond can be measured.
The CBC-R reconstruction method works for any kind of CBC padding oracles, although there are variations depending on the exact species of padding (in particular whether the decryption engine checks that all x last bytes have the same value or not). This can be applied wherever CBC-based decryption occurs without protection of a MAC. In the case of the Laravel framework, this was for cookies, and the lack of MAC was due to both improper computations, and the creative featurism of PHP. The same kind of padding oracle attacks has been applied in other contexts; the original description, back in 2002 (by Serge Vaudenay), was on SSL records. Rizzo and Duong popularized it in 2010 by showing how it applied well on ASP.NET.
This incidentally illustrates that a Javascript demo with a Youtube video can be a powerful path to fame even when the original research was done by somebody else 8 years ago. I guess this means that we need both really smart researchers like Serge, and determinate implementers who go to the trouble of understanding the research, and then applying it to practical cases, working out the zillions of practical implementation details. Theory and experimentation are two sides of Science and both are required to make things change.
Thank you for those who decided to read my long thread, I appreciate you sitting through it all, and hopefully you've learned something new :')
Last edited by ORLP2 on Wed Mar 25, 2015 6:45 pm; edited 1 time in total (Reason for editing : Brackets weren't needed.)

ORLP2- New Member
- Posts : 1
Join date : 2015-03-25
Page 1 of 1
Permissions in this forum:
You cannot reply to topics in this forum
 Home
Home
